Idealny filtr dolnoprzepustowy jest nieciągły w przestrzeni częstotliwości i rozciąga się nieskończenie w czasie. W grafice komputerowej, w filtrowaniu próbek obrazu podczas jego skalowania lub resamplingu musimy się posłużyć przyciętą w przestrzeni wersją sinc. Dla likwidacji oscylacji w jego widmie biorących się z nieciągłości powstałych w wyniku jego przycięcia musi zostać wymnożony z oknem. Jako okna używa się tego stworzonego przez niejakiego pana Lanczos - stąd nazwa filtru. Dlaczego takim oknem, a nie innym nie wiem. Okazało się także w trakcie eksperymentów, że najlepsze wyniki daje okno o wielkości 2 i 3.
Jedno o czym musimy pamiętać, że tworzenie filtrów to w pewnej mierze połączenie sztuki z nauką i dodatkowo to, że każdy ma inne gusta i inną percepcję. Filtr Lanczos jest prawie idealnym filtrem dolnoprzepustowym. Jednak wcale nie znaczy to najlepszym. Mówiąc o filtrowaniu obrazu chodzi nam o odcięcie wysokich częstotliwości, ale należy pamiętać, że oko nie postrzega widma (w przestrzeni, ale także samej fali elektromagnetycznej), poza tym receptory w oku nie są rozłożone równomiernie by eliminować możliwość aliasingu, sam mózg dokłada swoje w usuwaniu z postrzeganego obrazu niechcianych zakłóceń. Każdy ma inaczej rozłożone czopki w oku i inaczej utkane neurony i inny bagaż doświadczeń. Czopki u każdego reagują na tą samą częstotliwość fali trochę inaczej. Każdy ma inną optykę oka, inne zmętnienie soczewki. I pewnie można by tak wymieniać.
Oba filtry o szerokościach 2 i 3 mają dla pewnym wartości ujemne wartości, stąd istnieje możliwość, że wynikowa wartość splotu będzie ujemna. Czyli należy przewidzieć możliwość radzenia sobie z ujemnymi wartościami koloru. Przy samplowaniu Jitter dla niektórych metod resamplowania możemy otrzymać wartość koloru większą niż jeden.
Niezależnie od tego jak wygląda widmo filtru, jeśli filtr ma ujemne wybrzuszenia oznacza to, że będzie on miał właściwości wyostrzające.
Funkcja okna ma postać:
$\displaystyle W(x) = \begin{cases} \frac{sin \displaystyle\frac{x \pi}{\tau}}{\displaystyle\frac{x \pi}{\tau}} & \text{dla} \;\;\; -\tau \le x \le \tau \\ \\\\\\\\\\\\\\ \qquad 0 & \text{dla} \;\qquad |x|>\tau \end{cases}$
, gdzie $\tau$ to szerokość okna.
Po złożeniu z funkcją sinc otrzymujemy filtr:
$F(x) = \displaystyle \begin{cases} \frac{sin x \cdot sin \displaystyle\frac{x \pi}{\tau}}{x \cdot \displaystyle\frac{x \pi}{\tau}} & \text{dla } \;\;\; -\tau \le x \le \tau \\ \\\\\\\\\\\\\\\\\\\\ \qquad\qquad 0 & \text{dla } \;\qquad |x|>\tau \end{cases}$
Dla zera $\lim_{x \rightarrow 0}{\frac{sinx}{x}}\rightarrow 1$.
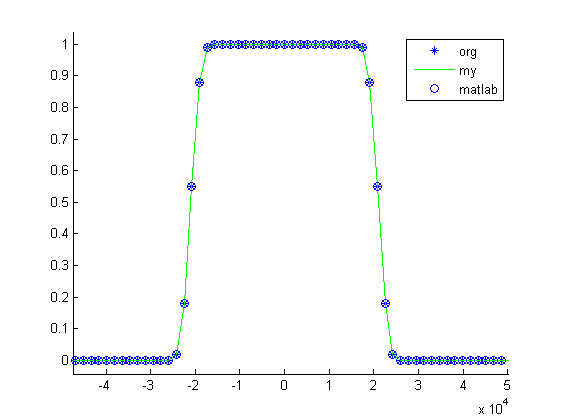
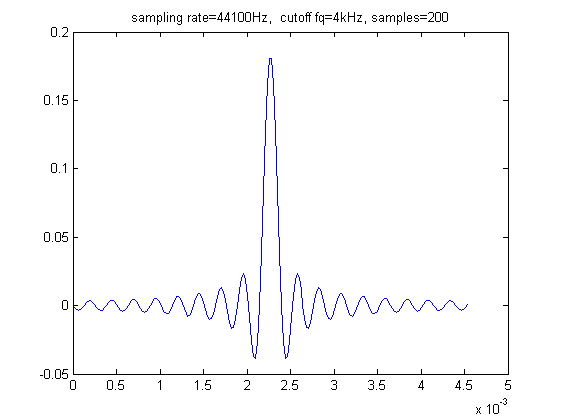
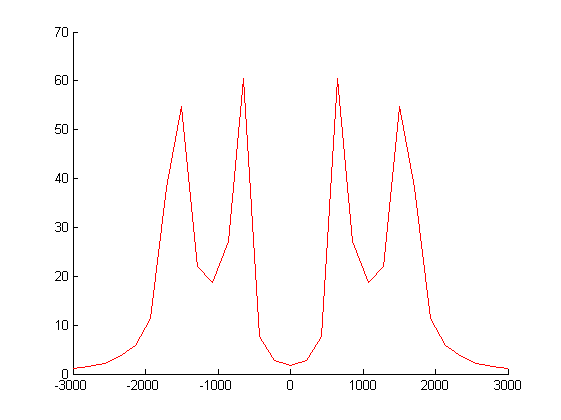
Dla $\tau=3$ wykresy filtru, okna, samej funkcji sinc mają postać:

Pole powierzchni filtra to 1, czyli dokonując z nim splotu nie zmieniamy energii sygnału.
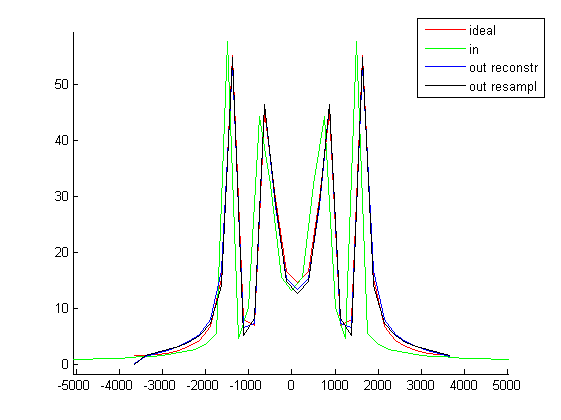
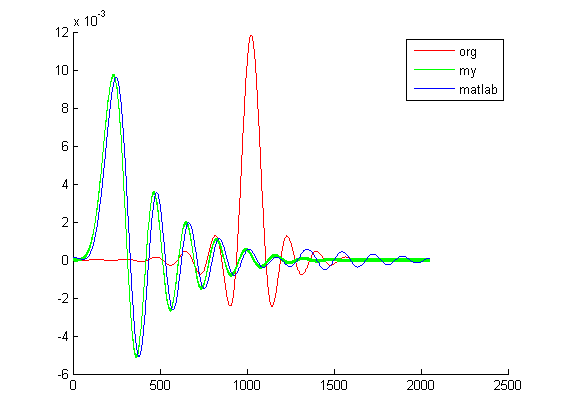
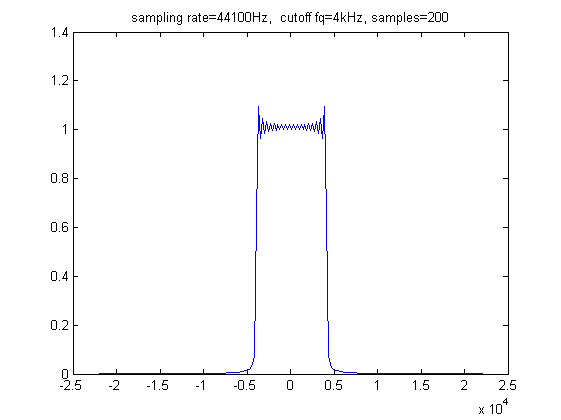
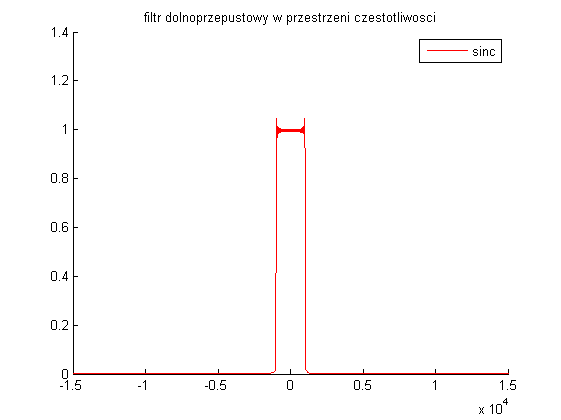
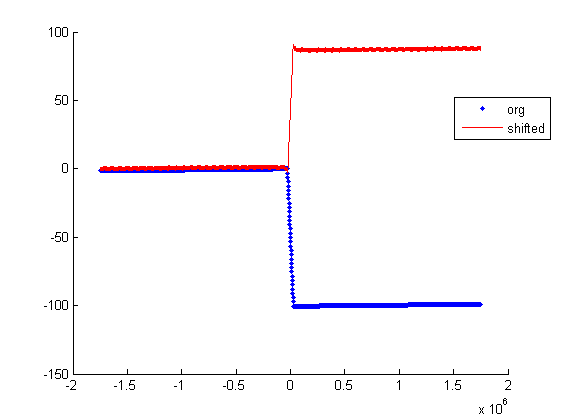
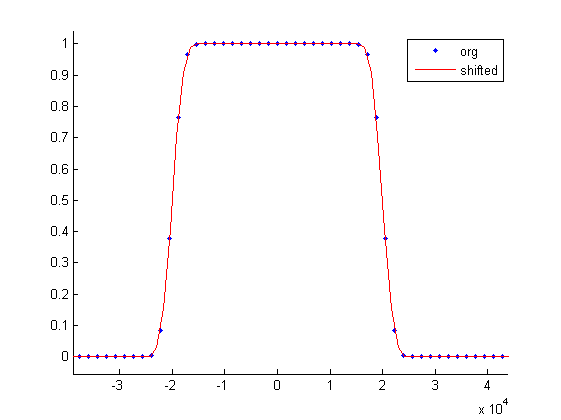
Porównanie widma funkcji przyciętej funkcji sinc bez i z oknem Lanczos:
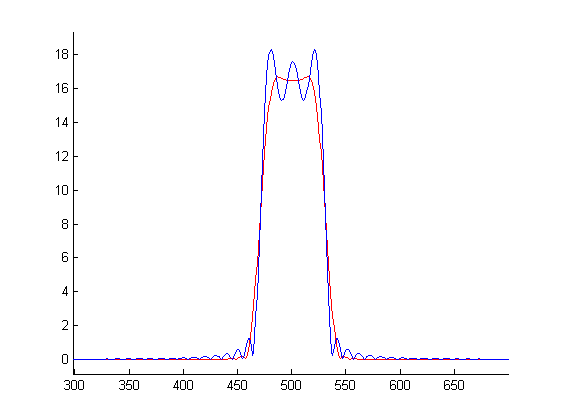
Filtr dwuwymiarowy $L(x,y)=L(x)*L(y)$ ma wygląd:

Jak widać nie powstaje on przez obrót filtru 1D. Objętość pod powierzchnią filtra 2D to jeden.
Przykładowy kod w Matlabie użytego do wygenerowania wykresów:
function [] = plot_lanczos()
x = linspace(-4, 4, 1000);
[y, ysinc, ywin] = lanczos(x, 3);
trapz(x, y)
figure(fig_index);
fig_index = fig_index + 1;
hold on;
plot(x, ywin, 'r o');
plot(x, y, 'b.');
plot(x, ysinc, 'g');
title('lanczos - spatial');
legend('window', 'lanczos', 'sinc');
x = linspace(-3, 3, 100);
[y, ysinc, ~] = lanczos(x, 3);
Y = fft(y, 1000);
YSINC = fft(ysinc, 1000);
figure(fig_index);
fig_index = fig_index + 1;
hold on;
title('lanczos - freq');
plot(fftshift(abs(Y)), 'r');
plot(fftshift(abs(YSINC)));
end
function [y, ysinc, ywin] = lanczos(tau)
y = zeros(1, size(x, 2));
ysinc = zeros(1, size(x, 2));
ywin = zeros(1, size(x, 2));
for i=1:size(y, 2)
xx = abs(x(i));
if (xx == 0)
ysinc(i) = 1;
ywin(i) = 1;
else
xx = xx * pi;
xxx = xx / tau;
ysinc(i) = sin(xx) / xx;
if (xx/pi <= tau)
ywin(i) = sin(xxx) / xxx;
end
end
y(i) = ysinc(i) * ywin(i);
end
end
function [] = plot_lanczos_3d()
N = 51;
tau = 3;
x = linspace(-tau, tau, N);
y = linspace(-tau, tau, N);
lx = linspace(-tau, tau, N);
ly = linspace(-tau, tau, N);
for i=1:N
lx(i) = lanczos(lx(i), tau);
ly(i) = lanczos(ly(i), tau);
end
[lx, ly] = meshgrid(lx, ly);
lz = lx .* ly;
surface(x, y, lz);
trapz(y, trapz(x, lz))
function [y] = lanczos(x, tau)
xx = abs(x);
if (xx == 0)
y = 1;
else
xx = xx * pi;
xxx = xx / tau;
ysinc = sin(xx) / xx;
ywin = 0;
if (xx/pi <= tau)
ywin = sin(xxx) / xxx;
end
y = ysinc * ywin;
end
end
endPrzykładowy kod klasy w C# implementujące filtr:
public class LanczosFilter : Filter
{
public double Tau = 3;
public override double Ray
{
get
{
return Tau;
}
}
public override double Evaluate(double a_value)
{
double v = Math.Abs(a_value);
if (v > Tau)
return 0;
if (v < Constants.DOUBLE_PRECISION)
return 1;
v = v * Constants.PI;
double p3 = v / Tau;
return Math.Sin(v) * Math.Sin(p3) / (v * p3);
}
}